قطع فاز یک سناریوی کابوسوار برای مهندسان سیستمهای قدرت است. اکثریت قریب به اتفاق عناصر حفاظت قطع فاز شبکه به گونهای طراحی شدهاند که وقتی جریان فاز بیش از حد وجود دارد کار کنند، اما در مورد یک هادی شکسته، عدم وجود جریان است که نگرانکننده است.
هادی های شکسته میتوانند باعث شروع آتش سوزی شوند و با تکنیکهای رله حفاظت از خطای زمین یا جریان اضافه معمولی شناسایی نشوند. خوشبختانه، درک فیزیک سناریوی شبکه حفاظت قطع فاز چندان دشوار نیست، و در حالی که توپولوژی شبکه توزیع سه سیم و چهار سیم، پاسخهای شبکه کمی متفاوتی را ارائه میدهند، درک صحیح از این مفاهیم به شناسایی و محافظت در برابر این سناریوی خطا کمک میکند.
اولاً، داشتن درک درستی از نظریه مؤلفه متقارن Fortescue، که میتوانیم از آن برای ترسیم جریانها و ولتاژهای اندازهگیری شده فاز به مؤلفههای توالی مثبت، منفی و صفر استفاده کنیم، ارزشمند است. این فرآیند نگاشت به ما این امکان را میدهد که عدم تعادل بین فازها را در طول خطا نادیده بگیریم و فرآیند تجزیه و تحلیل خطا را بسیار آسان تر میکند. اساساً، بیشتر تکنیکهای حفاظت از جریان متناوب (AC) از این فرآیند تبدیل برای شناسایی خطاها استفاده میکنند.
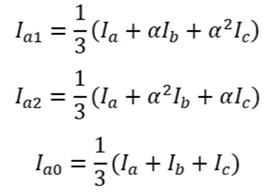
که در این فرمول:

با وارد کردن مقادیر برای هر اندازهگیری فاز، میتوانیم مقدار و فاز هر یک از اجزای دنباله را استخراج کنیم. در دنیای تئوری ایده آل، یک تغذیه کننده توزیع سالم نباید عدم تعادل را نشان دهد و بنابراین فقط باید دارای جریان توالی مثبت باشد. شما میتوانید این را با جایگزین کردن مجموعهای از فازهای جریان متعادل در معادلات تأیید کنید و ببینید که نتیجه برای هر معادله به جز دنباله مثبت صفر میشود.
در دنیای توزیع AC، اجزای متقارن تنها محدود به جریان نیستند. ولتاژها و امپدانسها همچنین میتوانند در قالب اجزای توالی نمایش داده شوند که تجزیه و تحلیل خطا را بسیار ساده میکند. این موضوع را میتوان جامعتر بررسی کرد اما زمانی که موضوع هادیهای شکسته را در نظر میگیریم، مهم است که اذعان کنیم:
- منابع ولتاژ به عناصر توالی مثبت محدود میشوند.
- امپدانس معادل مثبت، منفی و توالی صفر برای یک شبکه توزیع وجود دارد.
سیستم های سه سیم سه فاز برای حفاظت قطع فاز
هنگام در نظر گرفتن سناریوی قطع فاز، بیایید ابتدا در نظر بگیریم که در یک سیستم سه سیم(حفاظت قطع فاز) چه اتفاقی میافتد.
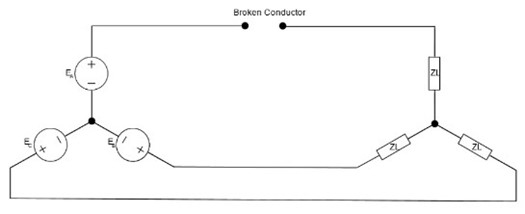
به عنوان اولین گام در تجزیه و تحلیل، ارزش درک اینکه قطع فاز برای هر یک از جریان های فاز چه معنایی دارد. با یک ناپیوستگی در فاز A، همانطور که در شکل بالا نشان داده شده است، به طور موثر جریان را از آن فاز حذف میکنیم. علیرغم تلاشهای ژنراتورهای 3 فاز برای عبور جریان از طریق خطوط، میتوانیم فرض کنیم که هیچ جریانی جریان نمییابد و باعث عدم تعادل واضحی برای ما میشود. میتوانیم مدار را به صورت زیر در نظر بگیریم کنیم:
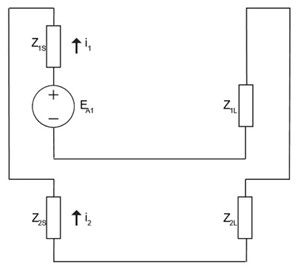
برای مهندس حفاظت ماهر، شکل بالا شباهت زیادی به تحلیل خطای یک خطای فاز به فاز دارد که به طور کلی منطقی است. در یک خطای فاز به فاز، فاز بدون خطا در مقایسه با خطای بین دو رسانا دیگر امپدانس نامحدودی دارد. تنها تفاوت این است که در خطای فاز به فاز، ما فقط امپدانس خط را در نظر میگیریم، در حالی که در سناریوی قطع فاز، امپدانس بار را در نظر میگیریم. بر اساس خطاهای فاز به فاز، برای سناریوی هادی شکسته در یک خط سه فاز، مدار معادل ما به صورت زیر میشود:
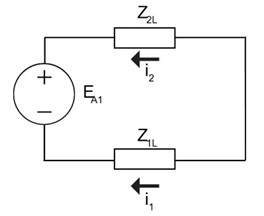
که چند نکته کلیدی به ما میدهند:
- در سناریوی قطع فاز، جریان توالی مثبت همان جریان دنباله منفی است. هنگامی که هادی شکسته نمیشود، 100٪ دنباله مثبت و 0٪ دنباله منفی آن است.
- جریانهای توالی مثبت و منفی با استفاده از امپدانس یکسان محاسبه میشوند.
- ممکن است بار همچنان به اندازهای زیاد باشد که i1 از سطح دریافت بیش از حد جریان تجاوز نکند – که خطرناک است.
رلههای حفاظت دیجیتال مدرن اغلب هم حفاظت توالی فاز منفی و هم حفاظت از جریان اضافه را ارائه میدهند. برای مورد سه سیم، میتوانیم ببینیم که جزء توالی فاز منفی مورد انتظار به امپدانس بار در سناریوی هادی شکسته وابسته است. بنابراین، جریان توالی منفی حاصله واقعی به توپولوژی بار در زمان خطا بستگی دارد. برای عملگرایی، میتوانیم در نظر بگیریم که در تئوری یک شبکه باید جریان توالی منفی بسیار پایینی را در حالت بدون خطا نشان دهد، بنابراین میتوانیم از این بهعنوان منطقی برای تنظیم نقطه عملیاتی برای NPS کاملاً پایین استفاده کنیم. این ممکن است در سناریوهای ساده کار کند، اما زمانی که درجه بندی حفاظتی بین چندین دستگاه مشکل ساز میشود، یک خطای فاز به فاز پایین دست در منطقه بعدی ممکن است به عنوان یک خطای NPS در منطقه بالادست ظاهر شود، که منجر به شرایط مسابقه بین NPS بسیار حساس در منطقه میشود.
هنگامی که اطلاعات امپدانس به سختی جمعآوری میشود، میتوانیم به رابطه i1 = i2 در یک سیستم 3 فاز در طول یک خطای هادی شکسته تکیه کنیم. هنگامی که یک هادی شکسته رخ میدهد، در یک مدل نظری کامل:
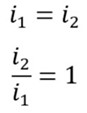
یا به صورت درصد بیان می شود:
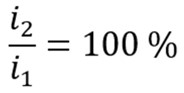
با اختصاص کد حفاظتی ANSI 46BC این نسبت دنباله منفی به مثبت، وابستگی امپدانس را از محاسبه حذف میکند. به این ترتیب، بدون توجه به بار، به شرایط خطای هادی شکسته حساسیت داریم. برای تشخیص موثر سناریوی هادی شکسته در یک شبکه سه فاز، و بسیار نادر است که هر سناریوی شبکه معمولی در یک شبکه سه فاز از 20٪ جریان توالی منفی به دنباله مثبت تجاوز کند. به این ترتیب، این یک تنظیم شروع معمول برای این ویژگی در این زمینه است که درجه بندی با عناصر اضافه جریان را ارائه میدهد و در عین حال موارد ناپیوستگی فاز را در نظر میگیرد.
سیستمهای چهار سیم سه فاز
متداول در توپولوژی های شبکه آمریکای شمالی و شبکه توزیع LV در استرالیا، چهار سیم سه فاز با در نظر گرفتن اثرات ناپیوستگی فاز، نتایج کمی متفاوت ارائه میدهد.
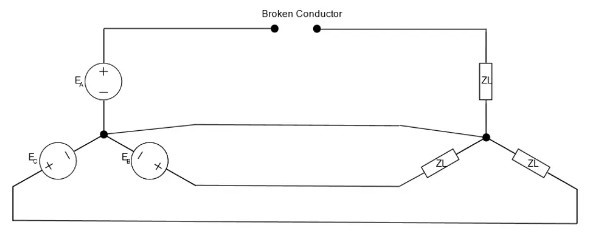
با اضافه کردن هادی خنثی، یک عارضه را به محاسبات وارد میکنیم زیرا در شرایط نامتعادل، نول تبدیل به هادی جریان میشود. غالباً این یک ملاحظات طراحی است و به دو سوم مشتریان در مورد LV اجازه میدهد تا در صورت مواجهه تک فاز با خطا، تداوم خدمات را به دو سوم مشتریان ارائه دهد، اما با اضافه کردن هادی نسبت i2 به i1 را در سناریوی هادی شکسته کاهش میدهیم. با یک هادی خنثی در حال بازی، ما اثر امپدانس دنباله صفر را معرفی میکنیم:
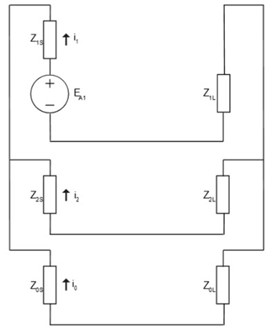
باز هم با یک شبکه معادل روبرو هستیم که بسیار شبیه به خطای Double Line to Ground است، با این تفاوت که به جای امپدانس خط، امپدانس بار را در نظر میگیریم. بیایید فرض کنیم که امپدانسهای منبع در مقایسه با بار ناچیز است، بنابراین در ساده سازی داریم:
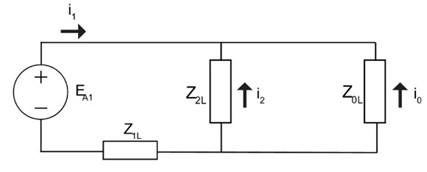
تفاوت کلیدی بین سیستمهای چهار سیم و سه سیم در گنجاندن دنباله صفر در محاسبه حاصل. محاسبه برای i1:
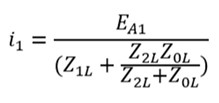
و با فرض منفی بودن i2 و تصدیق توپولوژی به عنوان یک تقسیم کننده جریان:
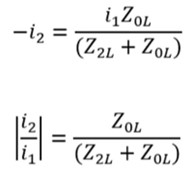
برای محاسبه حداقل حفاظت قطع فاز نسبت هادی شکسته در یک سیستم چهار سیمه، باید امپدانس بار توالی صفر و منفی را بدانیم. به عنوان یک قاعده کلی، امپدانس توالی صفر بیشتر از امپدانس دنباله منفی وجود دارد که باعث می شود |i2/i1| نسبت غیر صفر است، اما در غیاب اطلاعات امپدانس بار، بهتر است قبل از اعمال ویژگی 46BC، داده های میدانی را به صورت تجربی ارزیابی کنید. خدمات قبلی نشان میدهد که 20% |i2/i1| نسبت در شبکههای چهار سیمی برای حساسیت کافی است، اما در شبکههای بسیار نامتعادل از خطای کاذب مصون نیست.





بدون دیدگاه